swarnetz
The ground rules
A musical note at frequency 2f is perceived by the human ear as “the same note” as one at a frequency of f – except at a higher octave. For all music-theoretical purposes, these two are the same note, and in this article we’ll be operating under such an octave-invariant paradigm.
Two musical notes of frequencies p and q sound harmonious when p/q is a “small” rational number, since the first note’s q^th harmonic overlaps with the second note’s p^th harmonic.
While these ps and qs can have any prime factorization, for this article, we’ll be restricting ourselves to powers of 3 and 5, since these are both easy to tune on an instrument and occur in most commonly-heard music. A stretch goal would be to include 7.
A glimpse…
Thus, relative to a root node (tonic) with frequency f we can plot all natural tones in a subspace spanned by two “basis” harmonic relationships: 3f and 5f. In order to map these to a note we recogrnize, we’ll always be looking at values between the octave [f, 2f) and hence throwing around poers of 2 “for free”. Our “basis vectors” are now 3f/2 (= Pa or the perfect fifth) and 5f/4 (= Ga or the perfect third). The “negative axes” or inverse relationships in this case are 4f/3 = ma and 8f/5 = dha.
By “basis”, I mean that all the notes that we’ll ever consider, can be obtained by stringing together a series of these fractions. e.g. we find a Re at 9f/8 which is a Pa of the Pa.
The Tonnetz diagram adapted to Indian Classical Music
Western classical music uses the following diagram to visualize chords. The “basis vectors” described above are at 0 degrees and 60 degrees, and the reason these bases are tilted is because we can now visualize chords well (blue = major and red = minor).
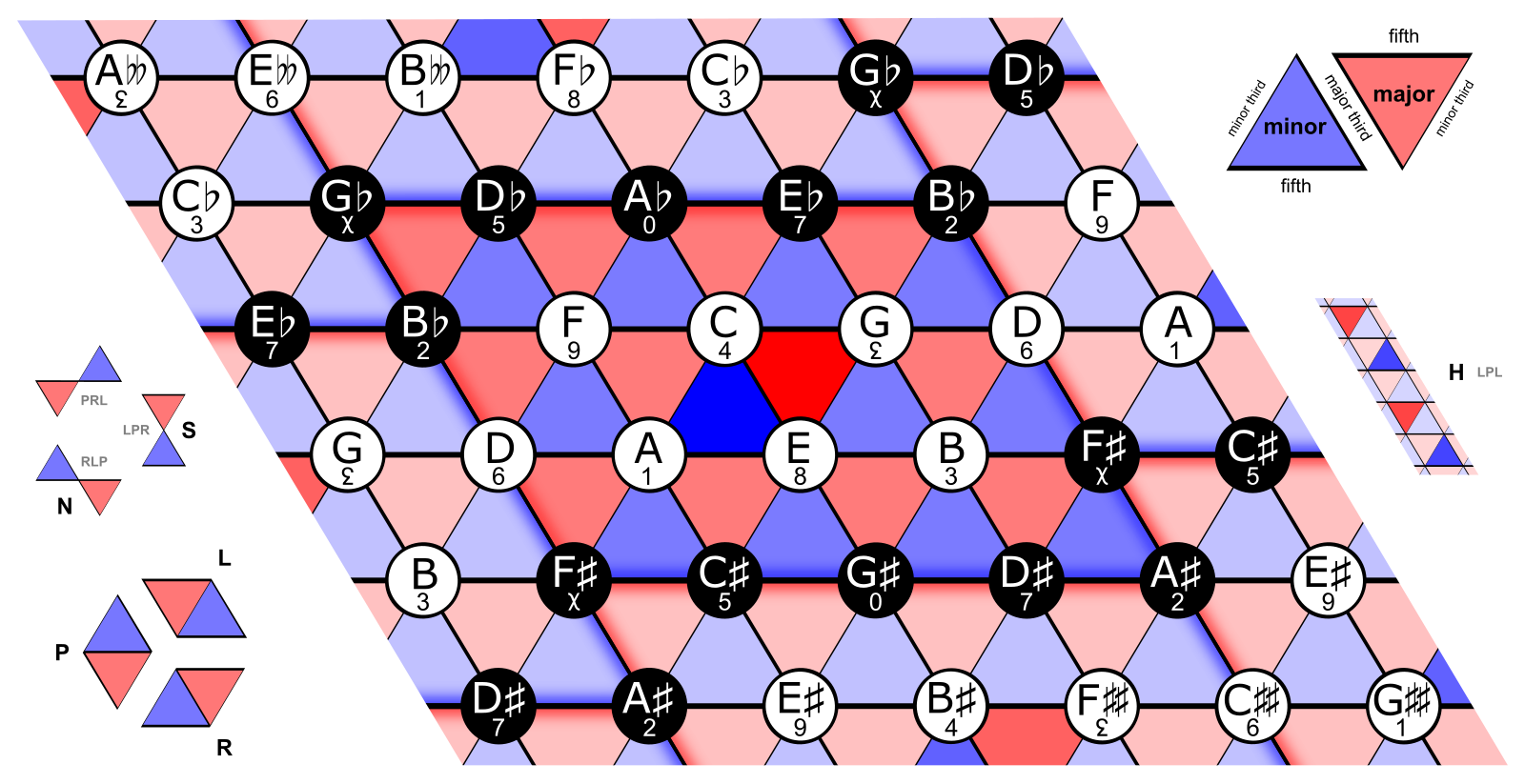
In ICM however, we have no reason to visualize chords and we’d like to stay in relative note notation, so our Tonnetz diagram will look like this:
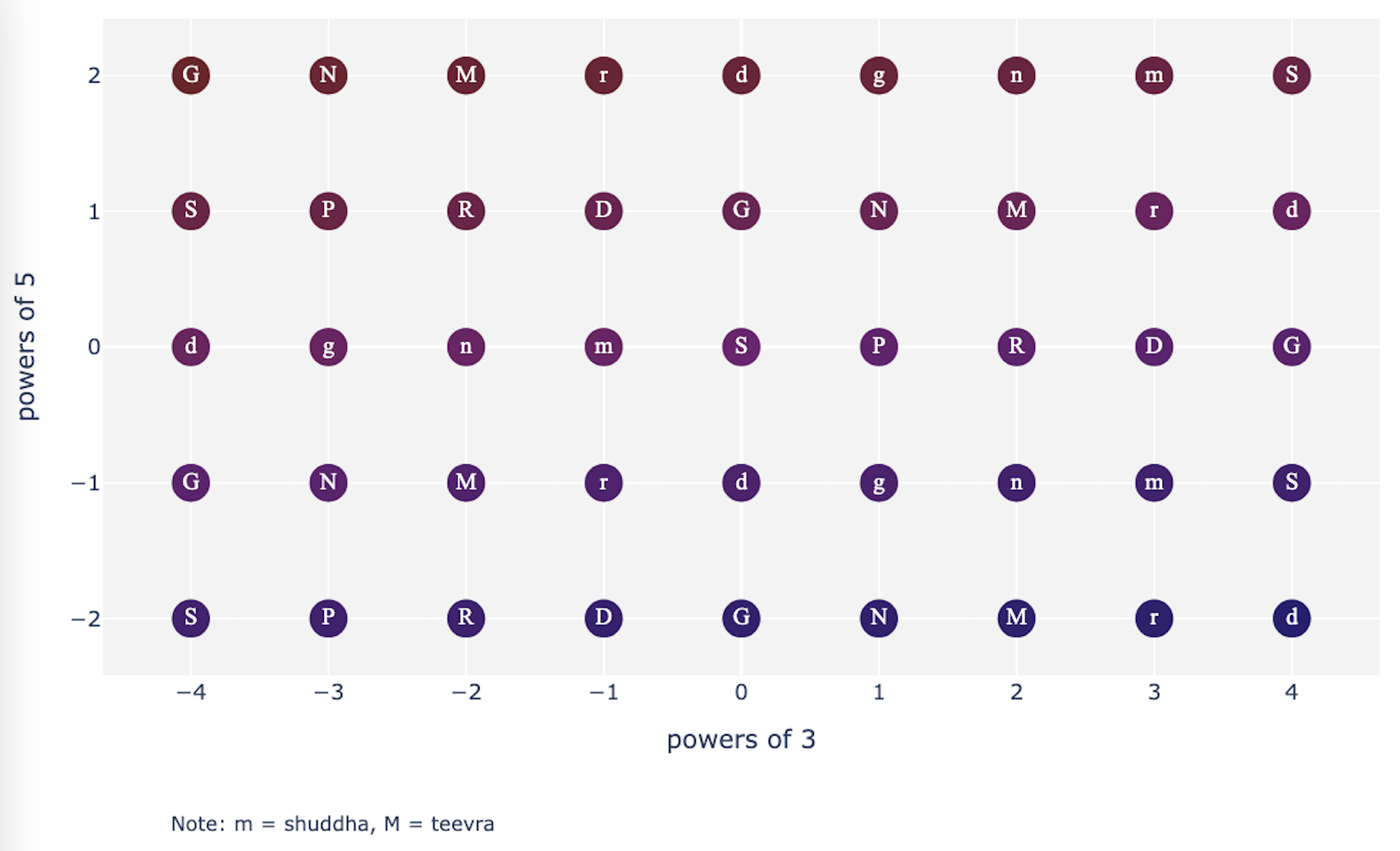
Raags
See this page for a list of raag shrutis as per what I have read, heard, and thought. These are not a definitive, and will be updated as I understand more.
References
- https://en.wikipedia.org/wiki/Tonnetz
- Dr Oak’s explanation of a Tonnetz net truncated at 22 nodes
- Dr Oak’s derivation of Shrutis in Raags
- A. Giri’s derivation of Shrutis in Raags
Categories: music
